Research: Number Theory

Fractional Derivatives of the Riemann zeta function

The video below shows the α-th Grünwald-Letnikov fractional derivative of the Riemann Zeta Function ζ(s) for α between 0 and 10 on -20 ≤ R(s) ≤ 20 and −3 ≤ I(s) ≤ 27.

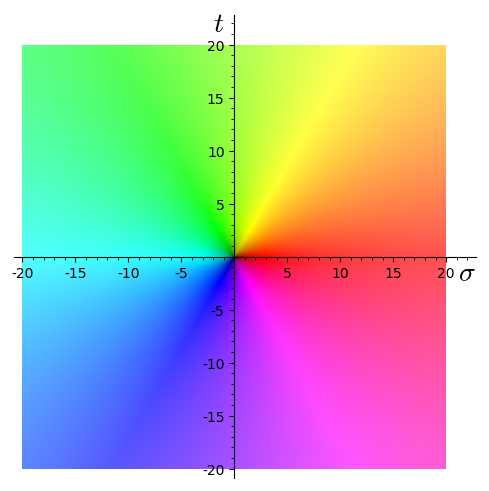
The hue represents the argument with red representing the positive real direction and cyan the negative real direction, as shown on the right. Brightness represents absolute value, with 0 represented by black and with white representing infinity. The plot on the right show the identity function.

Plots were generated with SageMath. For more see Zeros of Fractional Derivatives of Polynomials by Torre Caparatta, Sebastian Pauli and Filip Saidak. The video was complied with ffmpeg.