Research: Number Theory
Research
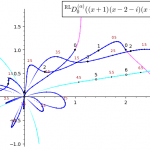
Zeros of Fractional Derivatives of Polynomials
We consider the polynomial p(x)=(x+1)(x-2-i)(x-3-i)(x-1-i) over the complex numbers. We have deg p′(x) = deg p(x)−1 = 4-1 = 3. The Fundamental…
Fractional Derivatives of the Riemann zeta function
The video below shows the α-th Grünwald-Letnikov fractional derivative of the Riemann Zeta Function ζ(s) for α between 0 and 10 on…
Interactive Sieve of Eratosthenes
Explore the sieve of Eratosthenes. Click on a number to have all its multiples marked by changing the field color to red…
Well-rounded forms and the Voronoi tessellation
One identifies the space of binary quadratic forms with the upper half plane $$\mathfrak{h}$$. The set of well-rounded forms corresponds to an…
Hermite Constants for Real Quadratic Fields
The Hermite constant for the ring of integers in real quadratic fields $$\mathbb{Q}(\sqrt{d})$$ for square-free positive integers $$d$$ are plotted above. The…
Extensions of the $$p$$-adic field $$\mathbb{Q}_p$$ with Galois group $$E_1$$
Let $$p$$ be an odd prime number. The graph shows the subgroup lattice of the group $$E_1$$, which is the unique non-abelian…
Congruence Subgroups of $$\textrm{PSL}(2,\mathbb{Z})$$
^ Level 19 Name Index con len c2 c3 > Cusps Gal Supergroups Subgroups 19A14 285 1 285 5 6 1915 61 91 1815 19A2…
Involve — a journal of mathematics
The mathematics journal Involve is dedicated to showcasing and encouraging high quality mathematical research involving students (at all levels). The editorial board consists of…
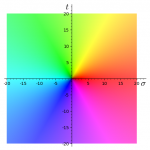
Riemann zeta Function $$\zeta$$ and its Derivative $$\zeta’$$
The absolute value of the Riemann zeta function $$\zeta(\sigma+it)$$ for $$0 \le \sigma \le 8$$ and $$0.1 \le t \le 60$$ over…
Zeros and Zero-Free Regions of $$\zeta^{(38)}$$
The plot shows the distribution of the zeros of the 38th derivative of the Riemann zeta function on the complex plane with…





