Research: Number Theory

Riemann zeta Function $$\zeta$$ and its Derivative $$\zeta’$$

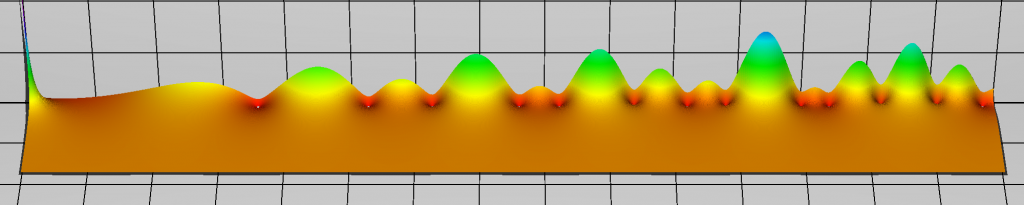
The absolute value of the Riemann zeta function $$\zeta(\sigma+it)$$ for $$0 \le \sigma \le 8$$ and $$0.1 \le t \le 60$$ over the complex plane. The white dots in the valleys are the non trivial zeros of the function. The Riemann hypothesis claims that the real part of all these zeros is $$1/2$$.

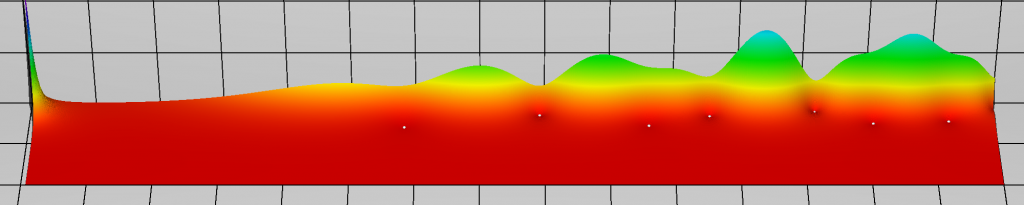
The absolute value of the derivative $$\zeta'(\sigma+it)$$ of the Riemann zeta function for $$0 \le \sigma \le 8$$ and $$0.1 \le t \le 60$$. The white dots in the valleys are zeros of the function. Both functions were plotted with the computer algebra system Sage.