Research: Number Theory

Zeros of the derivatives of the Riemann zeta function

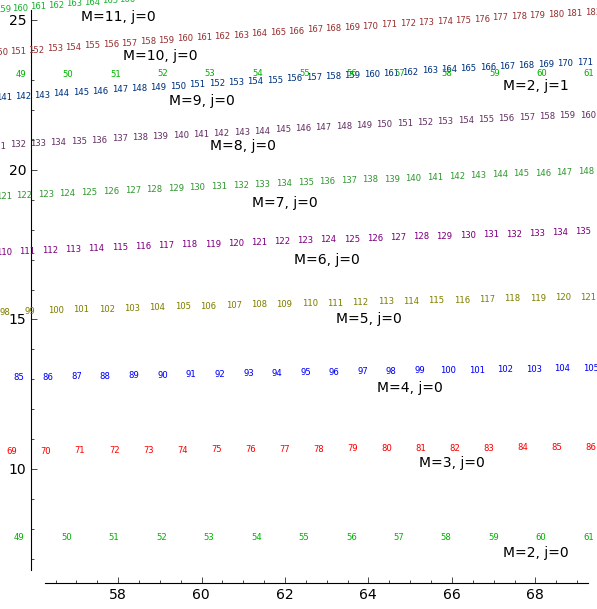
The plot shows zeros k of the derivatives $$\zeta^{(k)}(\sigma+it)$$ of the Riemann Zeta functionon the complex plane. In 1965 Spira had already noticed that the zeros of $$\zeta'(s)$$ and $$\zeta”(s)$$ seem to come in pairs, where the zero of $$\zeta”(s)$$ is always located to the right of the zero of $$\zeta'(s)$$. With the help of extensive computations, Skorokhodov (2003) observed this behavior for higher derivatives as well. For large $$k$$ and $$\sigma$$ this phenomenon is proven in New Zero-Free Regions for the Derivatives of the Riemann Zeta Function by Thomas Binder, Sebastian Pauli, and Filip Saidak.