Research: Number Theory

Zeros of Fractional Derivatives of Polynomials

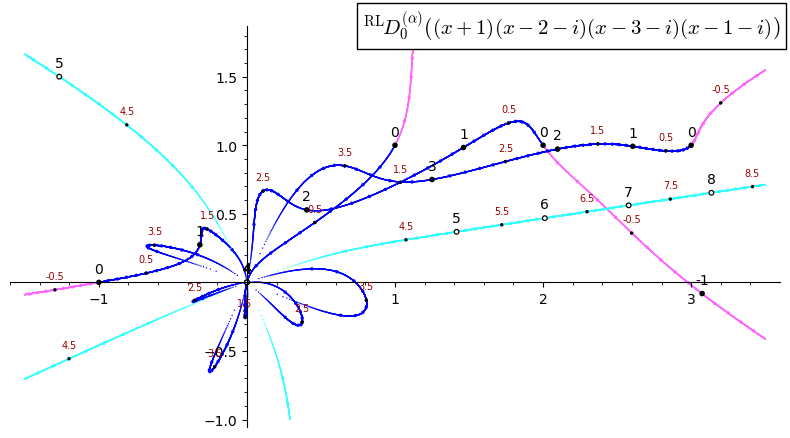
We consider the polynomial p(x)=(x+1)(x-2-i)(x-3-i)(x-1-i) over the complex numbers. We have deg p′(x) = deg p(x)−1 = 4-1 = 3. The Fundamental Theorem of Algebra asserts that the same reduction occurs for the total number of zeros of the polynomials. When we consider the fractional derivatives the following questions arise:

• What happens to the zeros of fractional derivatives, as the real α increases continuously from 0 to n ?
• How do the zeros of polynomials vanish ?

The video below shows the α-th Riemann-Liouville fractional derivative of the polynomial (x+1)(x-2-i)(x-3-i)(x-1-i) for -1< α < 9.

The hue represents the argument with red representing the positive real direction and cyan the negative real direction, as shown on the right. Brightness represents absolute value, with 0 represented by black and with white representing infinity.

Plots were generated with SageMath. The video was complied with ffmpeg.

For more see, Zeros of Fractional Derivatives of Polynomials by Torre Caparatta, Sebastian Pauli and Filip Saidak

We show the paths of the roots in the following plot.