1st UNCG PDE Conference 2021

Douglas Arnold
Complexes from complexes
Abstract: The finite element exterior calculus has highlighted the importance of Hilbert complexes to partial differential equations and their numerical solution. Hilbert complexes arise throughout mathematical physics. The fundamental partial differential operators from which most models in continuum physics are built may be realized as unbounded operators mapping between Sobolev and related Hilbert spaces, and these spaces and operators assemble into chain complexes. The resulting structure is a Hilbert complex : a finite sequence of Hilbert spaces together with closed unbounded operators from one space to the next such that the composition of two consecutive operators vanishes. This is a rich structure which combines functional analysis with homological algebra.
The most canonical and most extensively studied example of a Hilbert complex is the de Rham complex, which is what is required for application to fluid mechanics, electromagnetics, the Hodge Laplacian, and numerous other problems. This may give the impression that the finite element exterior calculus is only another way to look at these applications, which can be approached with less complicated machinery. But, in fact, there are many other important differential complexes as well, with applications to elasticity, plates, incompressible flow, general relativity, and other areas. These complexes are less well known and in many cases their properties, including properties needed to fit them into the finite element exterior calculus framework, have not been established.
In this talk I will discuss a systematic procedure for deriving such complexes and establishing their crucial properties.

Alfonso Castro
Multiplicity of solutions for quasilinear singular ordinary differential equations
Abstract: Motivated by the study of radial solutions to boundary value problems defined by perturbations of p-Laplacian equations we will discuss the role of energy functions, Pohozaev identities, phase plane analysis and blow-up solutions in the existence of multiple solutions to two-point boundary value problems. We will emphasize recent results where the perturbation includes a weight function such that the problem may be superlinear in a subregion but sublinear in its complement. Related results will be presented by Professors Jorge Cossio and Carlos Velez.

Mónica Clapp
Optimal partitions for the Yamabe equation
Abstract: The Yamabe equation on a Riemannian manifold (M,g) is of relevance in differential geometry. A positive solution to it gives rise to a metric on M which has constant scalar curvature and is conformally equivalent to the given metric g.
An optimal \ell-partition for the Yamabe equation is a cover of M by \ell pairwise disjoint open subsets such that the Yamabe equation with Dirichlet boundary condition has a least energy solution on each one of these sets, and the sum of the energies of these solutions is minimal.
We will present some recent results obtained in collaboration with Angela Pistoia (La Sapienza Universit‡ di Roma) and Hugo Tavares (Universidade de Lisboa) that establish the existence and qualitative properties of such partitions.

Xiaobing Feng
Recent developments in numerical fully nonlinear second-order PDEs
Abstract: Fully nonlinear PDEs are referred to as the class of nonlinear PDEs which are nonlinear in the highest order derivatives of the unknown functions appearing in the equations, they arise from many fields in science and engineering such as astrophysics, antenna design, differential geometry, geostrophic fluid dynamics, materials science, mathematical finance, meteorology, optimal transport, and stochastic control. This class of PDEs is known to be difficult to analyze analytically and to approximate numerically. In this talk, I shall first present a brief overview about some latest advances in numerical fully nonlinear PDEs and then discuss in detail a newly developed narrow-stencil finite difference and discontinuous Galerkin framework for approximating viscosity (and smooth) solutions of fully nonlinear second-order PDEs (such as Hamilton-Jacobi-Bellman and Monge-Ampere equations). The focus of the talk will be on discussing various numerical approaches/methods/ideas and their pros and cons for constructing numerical methods which can reliably approximate viscosity (and smooth) solutions of fully nonlinear second-order PDEs. Sample numerical experiments and application problems will also be presented.

Peter Poláčik
Quasiperiodic solutions of elliptic equations on the entire space via center manifold and KAM theorems
Abstract: In this project, we consider positive solutions of nonlinear elliptic equations on the Euclidean space of N+1 dimensions with some predetermined behavior (such as decay and symmetry) in the first N variables. We examine the behavior of these solutions in the remaining variable. Families of solutions periodic in the last variable have been found by several authors; our goal is to prove the existence of quasiperiodic solutions. In the lecture, I will discuss some general techniques based on center manifold and KAM theorems that we are using for this goal. Then I will report on recent progress. This is joint work with Dario Valdebenito.

Beatrice Rivière
Convergence of numerical methods for porous media flows
Abstract: Simulations of two-component single phase flows and two-component two-phase flows in heterogeneous porous media at the Darcy scale are important in the understanding of flow and transport processes in subsurface. Applications include storage of carbon dioxide in saline aquifers and production of hydrocarbons from oil and gas reservoirs. Mathematical models are based on conservation of mass for each fluid component. Models are characterized by systems of nonlinear coupled partial differential equations. In this talk, we formulate finite element and discontinuous Galerkin methods for the miscible displacement and incompressible two-phase flow problems. Challenges in the numerical analysis arise from the nonlinearity and the unboundedness or degeneracy of some of the PDE coefficients. Recent advances on the theoretical convergence of the proposed schemes for the discretization of the mathematical models in the general case are presented. Accuracy and robustness of the numerical methods for heterogeneous porous media are demonstrated.

Schedule (Eastern Daylight Time – GMT: -4)

7/24 Saturday

10:00 – 10:15am: Welcome remarks by Rich Fabiano and Musical performance by UNCG School of Music students by Ian T. Jones and Yesenia Josefsberg (Click Here for the YouTube Link)
10:15 – 10:30am: Welcome remarks by Terri Shelton, Vice Chancellor for Research and Engagement, and Sat Gupta, Head, Department of Mathematics and Statistics
10:30 – 11:30am: Plenary Lecture by Douglas Arnold “Complexes from complexes”
11:45am – 12:45pm: Plenary Lecture by Peter Polácik “Quasiperiodic solutions of elliptic equations on the entire space via center manifold and KAM theorems”
*BREAK*
1:40 – 3:20pm: Contributed Talks (Parallel Sessions 1-5 in Breakout Rooms)
3:30 – 4:30pm: Plenary Lecture by Beatrice Rivière “Convergence of numerical methods for porous media flows”

7/25 Sunday

10:30 – 11:30am: Plenary Lecture by Mónica Clapp “Optimal partitions for the Yamabe equation”
11:45am – 12:45pm: Plenary Lecture by Xiaobing Feng “Recent developments in numerical fully nonlinear second-order PDEs”
*BREAK*
1:40 – 3:20pm: Contributed Talks (Parallel Sessions 6-10 in Breakout Rooms)
3:30 – 4:30pm: Plenary Lecture by Alfonso Castro “Multiplicity of solutions for quasilinear singular ordinary differential equations”
4:30 – 4:45pm: Closing remarks and instructions for conference proceedings

7/24 Saturday (Eastern Daylight Time)

1:40 – 3:20p (20 mins for each talk: 15 mins talk + 5 mins question)

Session 1 – Chair: Sijing Liu
1:40 – 2:00p: Ravindran, S.S. “Analysis of stabilized Crank-Nicolson time-stepping scheme for the evolutionary Peterlin viscoelastic model”
2:00 – 2:20p: Cho, M. “A meshless method for regularized Laplacian boundary value problems using Steklov eigenfunctions”
2:20 – 2:40p: Sandilya, R. “Numerical stabilization of the Boussinesq system using boundary feedback control”
2:40 – 3:00p: Marazzato, F. “Discontinuous Galerkin implementation of variational phase-field models of brittle fracture”
03:00 – 03:20p: Liu, S. “A P_1 finite element method for a distributed elliptic optimal control problem with a general state equation and pointwise state constraints”

Session 2 – Chair: Ujjal Das
1:40 – 2:00p: Kumar, D. “Sobolev and Holder regularity results for some non-homogeneous quasilinear singular problems”
2:00 – 2:20p: El Aidi, M. “On a new parabolic Sobolev embedding map”
2:20 – 2:40p: Biswas, N. “On cylindrical and non-cylindrical (p,q)-Hardy potentials”
2:40 – 3:00p: Lopera Arias, E. J. “A generalized Pohozaev Identity: some applications”
3:00 – 3:20p: Das, U. “On the optimal space of Hardy potentials” 

Session 3 – Chair: Dhruba Adhikari
1:40 – 2:00p: Agudelo, O. “An existence result for anisotropic quasilinear problems”
2:00 – 2:20p: Taarabti, S. “Multiple solutions for a Neumann problem type with indefinite weight”
2:20 – 2:40p: Restrepo, D. “On the regularity and qualitative properties of solutions of Grad equations”
2:40 – 3:00p: Herrón O., S. “Infinitely many non-radial solutions of elliptic weighted superlinear problems”
3:00 – 3:20p: Adhikari, D.R. “A topological degree theory for perturbed A_G(S_+)-operators and applications to nonlinear problems”

Session 4 – Chair: Elliott Hollifield
1:40 – 2:00p: Shao, Y. “The fractional porous medium equation on manifolds with conic singularities”
2:00 – 2:20p: Kumar, U. “Sign-changing solutions to fractional p-Laplacian problem with purely critical nonlinearity in symmetric domain”
2:20 – 2:40p: Lan, K. “Hammerstein integral operators involving the Newtonian potential kernel” 
2:40 – 3:00p: Salazar, D. “Sign-changing concentrated solutions for a Neumann problem in 3D with critical nonlinearity”
3:00 – 3:20p: Hollifield, E. “Radial Symmetry of Nonnegative Solutions to Fractional Laplacian Equations”

Session 5 – Chair: Jerome Goddard II
1:40 – 2:00p: Yang, B. “New upper estimate for positive solutions to a second order boundary value problem with a parameter”
2:00 – 2:20p: Fonseka, N. “Logistic growth model with U-shaped density dependent dispersal and matrix hostility”
2:20 – 2:40p: Muthunayake, A. “Modeling the effects of trait-mediated dispersal on coexistence of mutualists”
2:40 – 3:00p: Acharya, A. “Sigma-shaped bifurcation curves”
3:00 – 3:20p: Goddard II, J. “When is competition better than having the whole patch to yourself?”

7/25 Sunday (Eastern Daylight Time)

1:40 – 3:20p (20 mins for each talk: 15 mins talk + 5 mins question)

Session 6 – Chair: Aaron Rapp
1:40 – 2:00p: Awanou, G. “Discrete Aleksandrov solutions of the Monge-Ampere equation”
2:00 – 2:20p: Ferrari, M. “On the coupling of the curved virtual element method and the one-equation boundary element method for 2D exterior Helmholtz problems”
2:20 – 2:40p: Luong, T. “Minimizers for the Cahn-Hilliard energy functional under strong anchoring conditions”
2:40 – 3:00p: Guo, D. “Semi-Lagrangian forward methods for time-dependent nonlinear partial differential equations” 
3:00 – 3:20p: Rapp, A. “The consistency of the dual-wind discontinuous Galerkin methods”

Session 7 – Chair: Falko Baustian
1:40 – 2:00p: Sanjuán, A. “A priori bounds for radial solutions to elliptic equations approaching critical growth”
2:00 – 2:20p: Kumar, K.A. “A shape variation result via the geometry of the eigenfunctions”
2:20 – 2:40p: Dimou, H. “A new variant of Wilson’s functional equation on monoids”
2:40 – 3:00p: Valdebenito, D.A. “Log-radially quasiperiodic solutions to certain semilinear elliptic equations” 
3:00 – 3:20p: Baustian, F. “Basis properties of Fucík eigenfunctions”

Session 8 – Chair: Byungjae Son
1:40 – 2:00p: Halder, A.K. “Solutions of Yu-Toda-Sasa-Fukuyama equation using point and nonlocal symmetries”
2:00 – 2:20p: Joseph, A. “Positive solutions to superlinear semipositone problems on the exterior of a ball”
2:20 – 2:40p: Thomas, P.J. “A partial differential equation for the mean–return-time phase of planar stochastic oscillator”
2:40 – 3:00p: Son, B. “A uniqueness result for positive radial solutions to nonlinear elliptic systems on the exterior of a ball”
3:00 – 3:20p: Sarkar, A. “Three solutions for a weighted p-Laplacian problem”

Session 9 – Chair: Jorge I Cossio Betancur
1:40 – 2:00p: Kotrla, L. “Comparison principles in problems with p-Laplacian”
2:00 – 2:20p: Mohammed, A. “On the lower and upper bound of the ground state-energy for the p-Laplacian operators”
2:20 – 2:40p: Vélez, C. “Energy and blow-up analysis associated to radially symmetric quasilinear Dirichlet problems with indefinite weight”
2:40 – 3:00p: Sportelli, C. “On existence and multiplicity of solutions for quasilinear elliptic systems of gradient type with a supercritical growth”
3:00 – 3:20p: Cossio, J. “Phase-plane analysis to prove the existence of infinitely many radial solutions for a quasilinear Dirichlet problem with indefinite weight”

Session 10 – Chair: Catherine Payne
1:40 – 2:00p: Almusawa, H. “Some more closed-form invariant solutions and dynamical behavior of multiple solitons for the (2+1)-dimensional rdDym equation using the Lie symmetry approach”
2:00 – 2:20p: Robertson, T. “Cauchy problem for Keller-Segel systems in weighted mixed-norm spaces” 
2:20 – 2:40p: Wagley, M. “Non-standard compact discretization for Burger’s type non-linear equations”
2:40 – 3:00p: Payne, C. “Delay-dependent stability criterion for linear neutral systems with distributed delays”
3:00 – 3:20p: Wang, T. “Forced oscillation of viscous Burger’s equation in a bounded domain”

The combined proceedings of the 2021/2023 UNC Greensboro PDE Conference Series were published by the Electronic Journal of Differential Equations:

• Mohammed Ahrami, Zakaria El Allali; Lower bounds on the fundamental spectral gap with Robin boundary conditions. 
• Gerard Awanou; Discrete Aleksandrov solutions of the Monge-Ampere equation.
• Falko Baustian, Vladimir Bobkov; Basisness of Fucik eigenfunctions for the Dirichlet Laplacian.
• Manki Cho, Mauricio A. Rivas; On the L^2-orthogonality of Steklov eigenfunctions.
• Xiaobing Feng, Thomas Lewis, Kellie Ward; A narrow-stencil framework for convergent numerical approximations of fully nonlinear second order PDEs.
• Daniel X. Guo; Semi-Lagrangian forward methods for some time-dependent nonlinear partial differential equations.
• Rohit Kumar, Abhishek Sarkar; Multiple solutions for a weighted p-Laplacian problem.
• Thomas Lewis, Aaron Rapp, Yi Zhang; Penalty parameter and dual-wind discontinuous Galerkin approximation methods for elliptic second order PDEs.
• Timothy Robertson; Wellposedness of Keller-Segel systems in mixed norm spaces.
• Dario A. Valdebenito; On solutions arising from radial spatial dynamics of some semilinear elliptic equations.
• Zhuoru Chen, Taige Wang, Xiangfei Xie; Bilinear estimates posed in finite domains in 2D and 3D.
• Petr Girg, Lukas Kotrla, Anezka Svandova; p-Laplacian in phenomenological modeling of flow in porous media and CFD simulations.
• Ani Tumanyan; Normal solvability and Fredholm properties for special classes of hypoelliptic operators.
• Zhenbu Zhang; Traveling wave solutions for an epidemic model.

Main Editors: Richard Fabiano and Yi Zhang

Associate Editors: Maya Chhetri, Tom Lewis and Ratnasingham Shivaji

2021 Conference Summary and Feedback

The conference was sponsored by the UNC Greensboro Department of Mathematics and Statistics and Helen Barton Excellence Professorship Funds. It featured 6 plenary lectures by world renowned experts (Douglas Arnold, Alfonso Castro, Mónica Clapp, Xiaobing Feng, Peter Polácik, Beatrice Rivière) and 10 parallel contributed talk sessions with 47 presentations. In the opening ceremony, we broadcasted musical performances by UNCG School of Music students (Ian T. Jones and Yesenia Josefsberg) and invited Terri Shelton (Vice Chancellor for Research and Engagement) and Sat Gupta (Head, Department of Mathematics and Statistics) to give welcome remarks.

Demographics:

• 195 registered participants from 24 countries
• 23 recent PhD (within three years) recipients
• 56 graduate students

Select Survey Feedback:

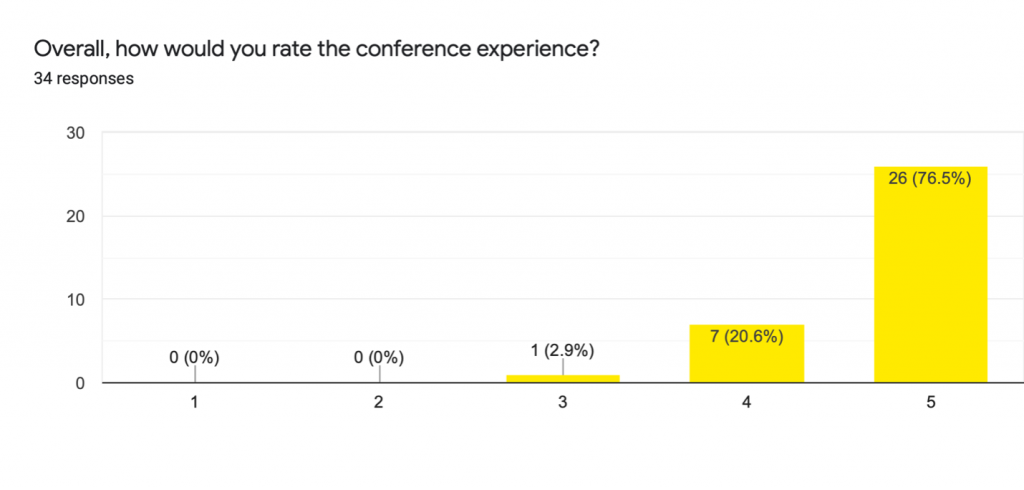
• It was good for us to see friends like Alfonso Castro
• Hoping that will have another conference either online or in person
• + Very nice introduction with history of UNCG and musical performance + Flow of conference was very good; timely, no lags. + Good variety of speakers/topics. Overall: Great conference 🙂
• This conference is an example on how online meetings should be.
• It is quite satisfactory to see that there are young people working on math.
• This conference is very beneficial for all the researchers.
• Very interesting
• Thanks and congratulaciones to the organizers.
• Wonderful event, I hope your invitation for any other, it was really nice. Thanks to all the organizers.
• This was an excellent conference. Lots of interesting talks on a wide variety of interesting topics.
• Excellent event. Excellent plenary speakers, perfect organization. I enjoyed it a lot. Many thanks to all organizers !!!
• Great conference!
• Thank you so much for nice conference

Sponsored by the UNC Greensboro Department of Mathematics and Statistics and Helen Barton Excellence Professorship Funds

Program Chair: Yi Zhang

Organizing Committee: Maya Chhetri, Rich Fabiano, Tom Lewis (Organizing Committee Chair), Yi Zhang, and Ratnasingham Shivaji

Technical Support: C. Matthew Farmer

Contact: Ratnasingham Shivaji – shivaji@uncg.edu