Research: Number Theory

Extensions of the $$p$$-adic field $$\mathbb{Q}_p$$ with Galois group $$E_1$$

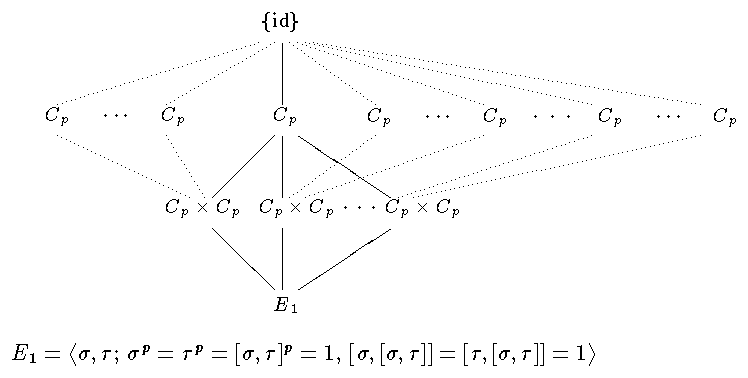
$Extensions of the $$p$$-adic field $$\mathbb{Q}_p$$ with Galois group $$E_1$$$

Let $$p$$ be an odd prime number. The graph shows the subgroup lattice of the group $$E_1$$, which is the unique non-abelian group of order $$p^3$$ of exponent $$p$$. $$C_p$$ denotes the cyclic group with $$p$$ elements.

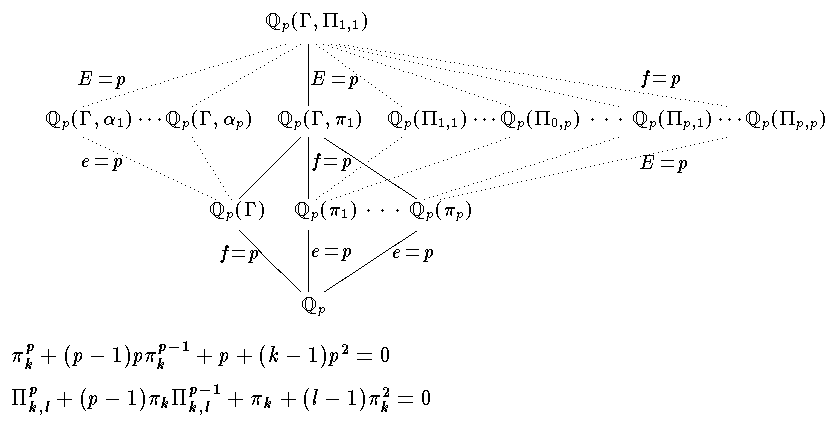
$Extensions of the $$p$$-adic field $$\mathbb{Q}_p$$ with Galois group $$E_1$$$

The subfield lattice of the unique extension of $$\mathbb{Q}_p$$ with Galois group $$E_1$$ with the minimal polynomials for the generating elements of the ramified (sub)extension of degree $$p$$. Furthermore inertia degrees $$(f=p)$$ and ramification indices $$(e=p,~E=p)$$ are given. A proof can be found in the thesis Efficient Enumeration of Extensions of Local Fields with Bounded Discriminant by Sebastian Pauli