Research: Applied Math

NSF Math Ecology Project

Collaborative Research: Mathematical & Experimental Analysis of Ecological Models: Patches, Landscapes, and Conditional Dispersal on the Boundary

Current team:

UNCG PI: Ratnasingham Shivaji.
UNCG Graduate Students: Quinn Morris, Catherine Payne.
UNCG Undergraduate Students: Jessica Nash.
External PIs: Jim Cronin (Louisiana State University), Jerome Goddard II (Auburn University Montgomery)
Other Collaborators: Stephen Robinson (Wake Forest University)

As part of a NSF-funded study “Mathematical and Experimental Analysis of Ecological Models: Patches, Landscapes and Conditional Dispersal on the Boundary,” we study the existence and multiplicity of solutions to the equation

where $$\lambda>0$$ is a real parameter, and $$\gamma>0$$ and $$0<A<1$$ are constants related to the quality of the surrounding environment and dispersal rate on the boundary, respectively.

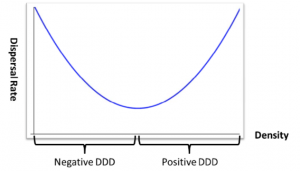(a) An example of U-shaped density dependent dispersal.	(b) The blue footed booby has been shown to exhibit both positive and negative density dependent dispersal depending on population density.
Figure 1: U-shaped density dependent dispersal.

Solutions to (0,1) are steady states of a reaction-diffusion equation which models a population with U-shaped density dependent dispersal on the boundary (i.e., high rates of dispersal when population size is very high or very low and low rates of dispersal for intermediate population sizes; see Figure 1. While the case of positive density dependent dispersal has been well researched, the case of negative density dependence has been treated in few cases and the case of U-shaped density dependence has not been treated at all. We study existence, multiplicity, and uniqueness results for certain ranges of the parameter $$\lambda$$ and explore how these results depend on the constant $$\gamma$$. Our theoretical results will be compared to experimental results of collaborators Jim Cronin and Rachel Harman of LSU (see Figure 2).

Figure 2: NSF-funded Mathematical Ecology Research Group: (a) Full research group at Cameron Jetties in January 2016; (b) LSU ecology collaborators at the field site; (c) Full research group at UNCG in June 2016.

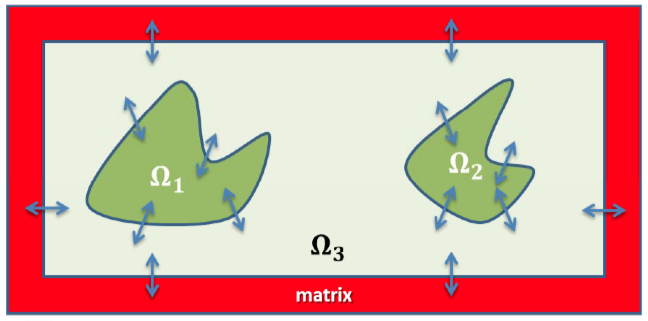
We aim to extend the model framework in order to study true landscape level dynamics of a population via a reaction diffusion system for a landscape model consisting of two patches, $$\Omega_1$$ and $$\Omega_2$$, separated by an intermediate matrix $$\Omega_3$$ that has the ability to maintain a small population (see Figure 3a). In particular, by extending the landscape model to the case of a two-dimensional landscape consisting of a disk $$\Omega_1$$ and an annulus $$\Omega_2$$, separated by an intermediate matrix $$\Omega_3$$ that has the ability to maintain a small population. The annulus $$\Omega_2$$ is then surrounded by a tunable hostile matrix (see Figure 3b). The framework will be sufficiently flexible as to allow different dynamics in each of the patches and the intermediate matrix, as well as conditional dispersal at each of the patch boundaries. I will study the structure of radially symmetric positive steady state solutions of the reaction diffusion based landscape model in concert with stability of the steady states. The same reaction terms and dispersal behaviors as before would be considered for study in this extension.

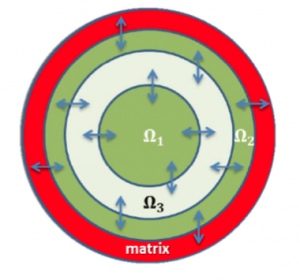Figure 3: Multiple patch models

Further adapting earlier models, we aim to develop a competing species reaction diffusion system to model competition mediated dispersal. In this case, two competing organisms occupy the same patch $$\Omega = \left \{ \ell x\ |\ x \in \Omega_0 \right \}$$ surrounded by a tunable hostile matrix. The main assumptions of the model are: 1) potential competitors have no effect on within-patch diffusion patterns, and 2) the emigration rate increases and/or the shape of the density-dispersal curve changes in the presence of an interspecific competitor. In other words, an unbiased random walk is assumed throughout the patch, while on the patch boundary organisms bias their movement in that their dispersal (emigration) from the patch is dependent on the density of the other organisms. I will then study the existence, nonexistence, uniqueness, multiplicity, and stability of positive steady state solutions of the model as the patch size $$\ell$$ and matrix hostility $$S^*$$ are both varied. Predictions of the persistence of the population will then be related to the biologically meaningful parameters providing crucial insight into the effects of habitat fragmentation and predation on the patch level dynamics of the population.

Related Publications

1. Analysis of steady states for classes of reaction diffusion equations with U-shaped density dependent dispersal on the boundary, Jerome Goddard II, Quinn Morris, Catherine Payne, Jordan Price, Stephen Robisnon, and R. Shivaji, Under preparation.
2. Stability analysis for positive solutions for classes of semilinear elliptic boundary value problems with nonlinear boundary conditions, Jerome Goddard II and R. Shivaji, accepted for publication, Proc. Royal Soc. Edin.
3. Diffusive logistic equation with constant yield harvesting and negative density dependent emigration on the boundary, Jerome Goddard II and R. Shivaji, J. Math. Anal. Appl., Vol. 414, 2014, No. 2, pp. 561–573.
4. Halo-shaped bifurcation curves in ecological systems, Jerome Goddard II and R. Shivaji, Electron. J. Diff. Equ., Vol. 2014, 2014, No. 88, pp. 1–27.
5. S-shaped bifurcation curves for logistic growth and weak Allee effect growth models with grazing on an interior patch, Dagny Butler, R. Shivaji, Anna Tuck, Electron. J. Differential Equations, Conf. 20, 2013, pp.15–25.
6. Existence of alternate steady states in a phosphorous cycling model, Dagny Butler, Sarath Sasi, and R. Shivaji, ISRN Mathematical Analysis, Vol. 2012, Article ID 869147, 12 pages, 2012.
7. A population model with nonlinear boundary conditions and constant yield harvesting, Jerome Goddard II and R. Shivaji, Proceedings of Dynamic Systems and Applications, Vol. 6, 2012, pp. 150–157.
8. An ecological model with $$\Sigma$$-shaped bifurcation curve, Eun Kyoung Lee, Sarath Sasi, and R. Shivaji. J. Nonlinear Analysis, Series B: Real World Applications, Vol. 13, 2012, No. 2, pp. 634–642.
9. Populations models with diffusion, strong Allee effect, and nonlinear boundary conditions, Jerome Goddard II, Eun Kyoung Lee, and R. Shivaji, J. Nonlinear Analysis, TMA, Vol. 74, 2011, No. 17, pp. 6202–6208.
10. $$S$$-shaped birufcation curves in ecosystems. Eun Kyoung Lee, Sarath Sasi, and R. Shivaji, J. Math. Anal. Appl., Vol. 381, 2011, No. 2, pp. 732–741.
11. Diffusive logistic equation with nonlinear boundary conditions, Jerome Goddard II, Eun Kyoung Lee, and R. Shivaji, J. Math Anal. Appl., Vol. 375, 2011, No. 1, pp. 365–370.
12. An ecological model with grazing and constant yield harvesting, Ryan Causey, Sarath Sasi, and R. Shivaji, Bulletin Belgium Mathematical Society, Vol. 17, 2010, No. 5, pp. 833–839.
13. Population models with nonlinear boundary conditions, Jerome Goddard II, Eun Kyoung Lee, and R. Shivaji, Electron. J. Differential Equations, Conf. 19, 2010, pp. 135–149.
14. Population dynamics with symmetric and asymmetric harvesting, Jaffar Ali, David Perry, Sarath Sasi, Jessica Schaefer, Brian Schilling, R. Shivaji, and Matthew Williams, Electronic Journal of Qualitative Theory of Differential Equations, Special Edition I, 2009, No. 2, pp. 1–16.
15. Population models with diffusion, strong allee effect, and constant yield harvesting, Jaffar Ali, R. Shivaji, and Kellan Wampler, J. Math Anal. Appl., Vol. 352, 2009, No.2, pp.907–913.
16. Persistence in reaction diffusion models with weak Allee effect, J. Shi and R. Shivaji, J. Math Biol., Vol. 52, 2006, No. 6, pp. 807–829.
17. Logistic equation with the $$p$$-Laplacian and constant yield harvesting, S. Oruganti, J. Shi, and R. Shivaji, Abstract and Applied Analysis, 2004, No. 9, pp. 723–727.
18. Diffustive logistic equation with constant yield harvesting, I: Steady States, S. Oruganti, J. Shi, and R. Shivaji, Trans. Amer. Math. Soc., Vol. 354, 2002, No. 9, pp. 3601–3619.